The Brachistochrone problem

    Anyone who has taken elementary math classes knows that the shortest distance between two points is a straight line. Therefore, when we try to get from point A to point B, we try to walk a straight line, because it is the shortest distance. However, is it true that a straight pathway is always the fastest way to get from point A to point B? Consider this situation. Imagine that there are three different slopes, they are all elevated to the same height above the ground, but their shapes are different. One slope is significantly curved, another one is mildly curved, the other one has a flat surface. When you release three identical balls from the top of these three slopes at the same time, which ball would reach the bottom of the slope first?

    I believe most of the people's answer would be the slope that has a flat surface because the distance from the top to the bottom of the slope is the shortest, which means the distance that the ball has to travel is the shortest, so the ball would rich the bottom in the least amount of time. Although it is true that the flat slope is the shortest pathway, it is not fastest. In this case, we have to consider the acceleration caused by the gravity. On these three different slopes, the accelerations of the balls are different. On the flat slope, the initial acceleration of the ball is relatively small. On the slope that is curved, the initial acceleration of the ball is relatively fast because the ball has greater verticle displacement in the beginning. Therefore, the ball on the curved slope moves faster than the ball on the flat slope in the beginning, when two balls reach the bottom, they would have the same speed. That's why the ball on the curved slope reach the bottom before the ball on the flat slope. However, it doesn't mean that the curve of the slope is inversely proportional to the time that balls take to reach the bottom. Although it is true that the ball accelerations faster when there's more curvature on the slope, it also means that the ball has to travel more distance to reach the bottom,

    If the flat slope and the extremely curved slope are both not the fastest pathways for the ball to reach the ground, then what is? Actually, scientists in the past had answered this question for us. They found that there's a specific curve that can make a ball reach the bottom of the slope in the shortest time. This curve is called "cycloid". A cycloid is a curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line without slippage.(Figure 1) Although there are many ways to prove that cycloid is the fastest pathway for a ball to reach the bottom of the slope. A scientist named Johann Bernoulli offered a clever solution. He used a principle called "Fermat's principle" to solve this problem. Fermat's principle states that the path taken between two points by a ray of light is the path that can be traversed in the least time. In addition to Fermat's principle, Snell's law is also a part of his solution. (Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air.)(Figure 2) According to the Snell's law light changes its direction to an angle when it passes two different isotropic media. Bernoulli realized that if we let a beam of light passes through infinite layers of different isotropic media, the path which light travels would be a curve, and that curve is the cycloid. (Figure 3)
Although there are some mathematical proves involved in this solution, I am not going to go over those. The concept I just mentioned is the main idea of Bernoulli's solution, and it is clever.

    The Brachistochrone problem is a very interesting aspect of physics and math. It also shows us that the fastest way is not always the straight line. Thinking about this problem can help us getting out of the old concepts and stop us from thinking intuitively.

Here's the link to a demonstration of the Brachistochrone problem:https://www.youtube.com/watch?v=GUcDyEZzcfA


Figure 1

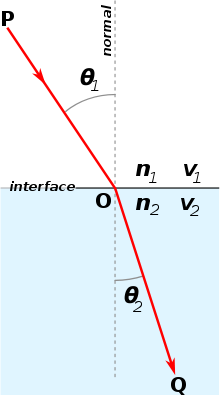
Figure 2

Figure 3